5 Frequenzanalyse
In diesem Unterrichtsblock lernen Sie mehr über die Frequenzanalyse von Messsignalen, und ihre Anwendungen: wir haben bisher Messsignale als Funktion der Zeit betrachtet, und gelernt wie man sie nach ihren Eigenschaften klassieren kann. Wir haben auch beim Thema Abtasten gelernt dass mit mehr als der doppelten Signalfrequenz abtasten muss (Abtasttheorem); besser noch mit der 10-fachen Frequenz des Signals. Dies bedingt aber, dass man dem Signal ansieht was für Frequenzen darin vorkommen. Bei einem Sinus ist dies noch einfach; bei einem allgemeinen periodischen Signal hingegen schwieriger.Viele Operationen die man mit Signalen durchführen möchte sind im Frequenzbereich einfacher durchzuführen und zu verstehen als im Zeitbereich, dazu gehört insbesondere die Filterung (Glättung) von Signalen. Daneben sind in der Mess- und Sensortechnik Anregungen mit harmonischen Signalen einer bestimmten Frequenz beliebt, gekoppelt mit einer Auswertung bei dieser bestimmten Frequenz - dies führt zu viel stabileren Signalen, wie ich Ihnen beim Thema Kraftmessung noch vorführen werde.
Repetition Fourieranalyse
Mittels Fourieranalyse findet man in einem Signal als Funktion der Zeit die zugehörigen Frequenzen. Sie haben die Fourieranalyse vermutlich in Analysis 3 kennengelernt und im Grundlagenlabor angewendet, als Sie mit einem Power Analyzer die Netzqualität untersucht haben. Schauen Sie zum Einstieg das Video mit einer Repetition zur Fourierreihe.
Fouriertransformation vs Fourierreihe
Im Video kommt die Fourierreihe vor, die nur für periodische Funktionen anwendbar ist. Aufgrund der Periodendauer \(T\) des periodischen Signals sind nur die Frequenzen \(f=1/T\) sowie alle ganzzahligen Vielfachen dieser Grundfrequenz möglich. Das sind zwar unendlich viele mögliche Frequenzen, aber die anderen Frequenzen (z.B. 0.7\(f\) etc) sind "verboten" oder ungebraucht.Für nichtperiodische Funktionen kann man die Fouriertransformation benützen, die nun das Signal als Summe von allen möglichen Frequenzen schreibt, d.h. nicht nur die ganzzahligen Vielfachen einer Grundfrequenz. Die Fouriertransformation ist also einfach eine Verallgemeinerung der Fourierreihe für nicht-periodische Funktionen.
Einführung Frequenzanalyse
Schauen Sie das Video mit Einführung zu der Frequenzanalyse.
Tiefpassfilter
Ein Tiefpassfilter ist ein Filter der tiefe Frequenzen passieren lässt, hohe Frequenzen hingegen blockiert. Er dient zum Beispiel dazu hochfrequentes Rauschen von einem niederfrequenten Signal zu trennen. Sie haben das Beispiel mit der U-Wert-Messung via 3-Temperatur-Messung bereits so ähnlich gesehen:
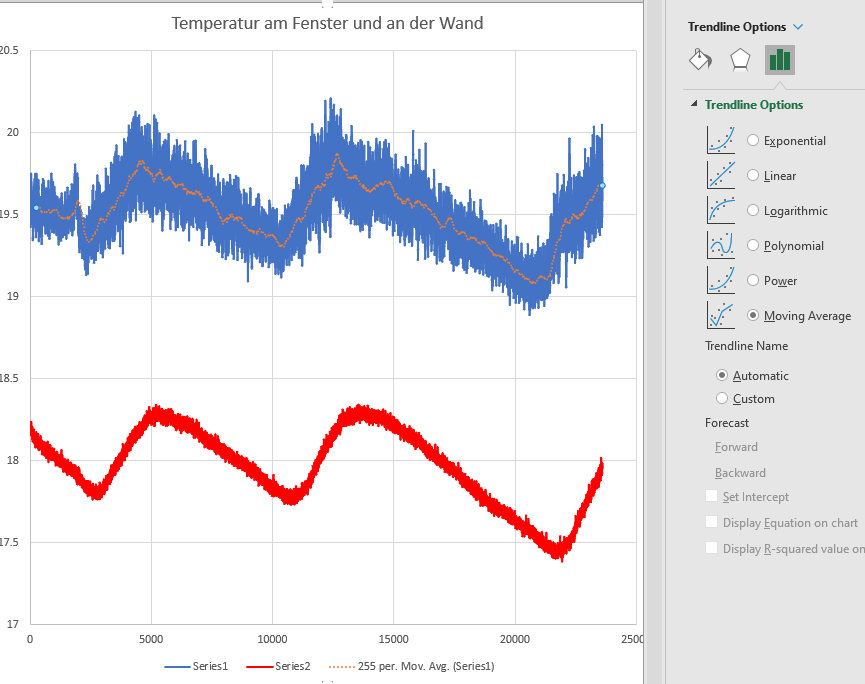
In der Übung wurde ein gleitender Mittelwert verwendet (orange innerhalb der verrauschten blauen Messdaten) um den Temperaturverlauf am Fenster "schöner" zu machen. Sie sehen in der Grafik dass das echte Signal, nämlich die langsame Temperaturänderung über die Zeit, eine Oszillation mit ca. 10'000 Sekunden "Periodendauer" aufweist. Es ist natürlich nicht periodisch, weil die Heizung nicht periodisch ein- und ausschaltet, manchmal etwas schneller, manchmal etwas langsamer - aber typischerweise schaltet sie alle paar Stunden ein. Das heisst dass im Nutzsignal (die geglättete Kurve) vermutlich Frequenzen vorkommen die tiefer sind als \(1/T\) mit \(T\) = 1 Stunde. Alle höheren Frequenzen haben mit der Heizung nichts zu tun und sind nur Rauschen. Man könnte also alle "schnellen" Änderungen (= schnell gegenüber den Änderungen im Nutzsignal) zu entsorgen versuchen, und das geht mit einem Filter der Frequenzen > 1/3600 Hz blockiert. In der Übung wurde ein gleitender Mittelwert verwendet, mehr als 255 Datenpunkte = 255 Sekunden war damit nicht möglich; und ein gleitender Mittelwert über 255 Sekunden würde zum Beispiel genau die Frequenz 1/255 Hz komplett blockieren (so wie die Integrationszeit im Multimeter die Netzstörung blockieren konnte, da genau über 1 Periode gemittelt wurde).
Gleitende Mittelwerte sind also eine Art Tiefpassfilter, aber nicht der "normalste" Typ Tiefpassfilter. Der allernormalste Tiefpassfilter ist Ihnen in der Vorlesung leicht verkleidet schon begegnet, und wird im nächsten Video vorgestellt und vorgeführt.
- Wie gross ist die Grenzfrequenz bei der "schwächsten" Einstellung des Tiefpassfilters? (\(R = 1k\Omega\; \quad C = 0.1 \mu F\))
- Bei welchem Wert von \(C\) (0.1,0.3,1,3,10,100 \(\mu F\)) ist man am nächsten bei einer Grenzfrequenz von 50 Hz?
Lösungen anzeigen
Am Schluss vom Video habe ich langsam die Grenzfrequenz des Tiefpassfilters kleiner gemacht. Welche zwei Effekte können Sie im grünen Signal (tiefpassgefiltert) beobachten?
Tipp anzeigen
Lösung anzeigen
Jetzt wird es spannend: Sie wollen den Tiefpassfilter einsetzen um die letzte Woche gezeigte Datenerfassung zu verbessern. Vor die
Datenerfassungskarte mit Tastfrequenz 100 Hz soll der Tiefpassfilter geschaltet werden. Was für eine Grenzfrequenz würden Sie einstellen?
Lösungen anzeigen
Tiefpassfilter und Abtasttheorem
Letzte Woche habe ich Ihnen vorgeführt wie die Datenerfassungskarte mit einer Tastfrequenz von 100Hz von Frequenzen grösser 50Hz in die Irre geführt wird, bzw. beispielsweise eine Frequenz von 90 Hz fälschlicherweise als 10Hz anzeigt. Die Lösung dafür ist dass man ein Tiefpassfilter vor die Datenerfassungskarte schaltet, das die höheren Frequenzen blockieren soll. Im nächsten Video mache ich den kombinierten Versuch mit der Datenerfassung via LabView mit 100Hz wie letzte Woche, aber nun noch mit einem Tiefpassfilter dazu.
Bei etwa 2:30 im Video ist der Tiefpassfilter auf \(R = 10k \Omega\) und \(C = 10 \mu F\) eingestellt.
Wie gross ist nun die Grenzfrequenz?
Ich lese bei 91 Hz eine Amplitude von etwa 0.02V ab, oder eine Unterdrückung um einen Faktor 50; bei 5Hz lese ich etwa 0.3 V ab, oder eine Unterdrückung um einen Faktor 3.
Wie stark wird das Signal bei 91 Hz etwa unterdrückt (Faktor wie viel kleiner ist es im LabView-VI als auf dem Oszilloskop)?
Wie stark wird das Signal bei 5 Hz etwa unterdrückt (ca. 3:00 im Video)?
Lösungen anzeigen
Versuchen Sie anhand der oben angegebenen Unterdrückungsfaktoren oberhalb der Grenzfrequenz eine allgemeine Gleichung anzugeben: Wie
gross ist der Unterdrückungsfaktor wenn das Signal N Mal höher ist als die Grenzfrequenz?
Lösung anzeigen
Wenn man zwei Tiefpassfilter erster Ordnung hintereinander schaltet erhält man einen Tiefpassfilter zweiter Ordnung (und wenn man drei hintereinanderschaltet, einen Tiefpassfilter dritter Ordnung usw. ). Wie stark unterdrückt ein Tiefpassfilter zweiter Ordnung ein Signal einer Frequenz die N Mal höher ist als seine Grenzfrequenz?
Lösung anzeigen
Viele Datenerfassungsgeräte haben eingebaute Tiefpassfilter, um die Störungen durch Aliasing zu verhindern, und auch im Datenerfassungsmodul das ich für diese Versuche verwendet habe ist dies nicht anders. Allerdings ist dieses Datenerfassungsmodul in der Lage mit bis zu 48'000 Samples/Sekunde zu arbeiten, also mit Samplingfrequenzen bis zu 48 kHz, d.h. es darf natürlich keinen Tiefpassfilter eingebaut haben der Frequenzen <24 kHz bereits unterdrückt, weil solche Frequenzen laut dem Abtasttheorem immer noch gemessen werden könnten.
Ganz allgemein sind fehlende (hohe Frequenzen werden falsch gemessen) oder vergessene Tiefpassfilter (höhere Frequenzen werden nicht richtig gemessen weil man vergessen hat dass irgendwo ein Tiefpassfilter ist) bei der Datenerfassung oft ein Problem.
Hochpassfilter
Neben Tiefpassfiltern gibt es noch weitere Filter; ein Filter der hohe Frequenzen passieren lässt aber tiefe Frequenzen blockiert heisst Hochpassfilter. Diese Filter werden eingesetzt wenn ein Signal langsam driftet z.B. mit der Umgebungstemperatur oder der Luftfeuchtigkeit (beides Störgrössen die sich nur langsam ändern), und wenn das Signal selber sich deutlich schneller ändert als diese langsamen Änderungen der Umgebung.
Sie haben bereits gesehen wie man einen Tiefpassfilter als frequenzabhängigen Spannungsteiler bauen kann. Wie könnte man elektronisch einen Hochpassfilter konstruieren?
Lösung anzeigen
Der Hochpassfilter wird im folgenden Video vorgeführt.
Bandpassfilter
Man kann nun auch noch ein Hochpassfilter und ein Tiefpassfilter miteinander kombinieren (anstatt wie oben, 2 Tiefpassfilter). Nimmt man beispielsweise ein Hochpassfilter mit Grenzfrequenz 10 Hz (alles über 10 Hz kommt durch), sowie ein Tiefpassfilter mit Grenzfrequenz 20 Hz (alles unter 20Hz kommt durch), so lässt diese Kombination die Frequenzen zwischen 10 und 20 Hz durch, und blockiert die übrigen Frequenzen.Bandpassfilter sind in der Messtechnik besonders interessant, weil man oft ein Signal künstlich bei einer bestimmten Frequenz erzeugt. So kann man z.B. einen Streulichtsensor mit einer gepulsten Lichtquelle mit Frequenz f bauen, und weiss damit dass das Nutzsignal aus dem Streulichtdetektor ebenfalls bei dieser Frequenz sein muss. Andere Frequenzen im Signal können "entsorgt" werden, d.h. man benützt dann ein sehr schmalbandiges Bandpassfilter um die Frequenz \(f\) (schmalbandig heisst: es lässt ausser der Frequenz \(f\) nur einen ganz kleinen weiteren Frequenzbereich durch).
Zusammenfassung
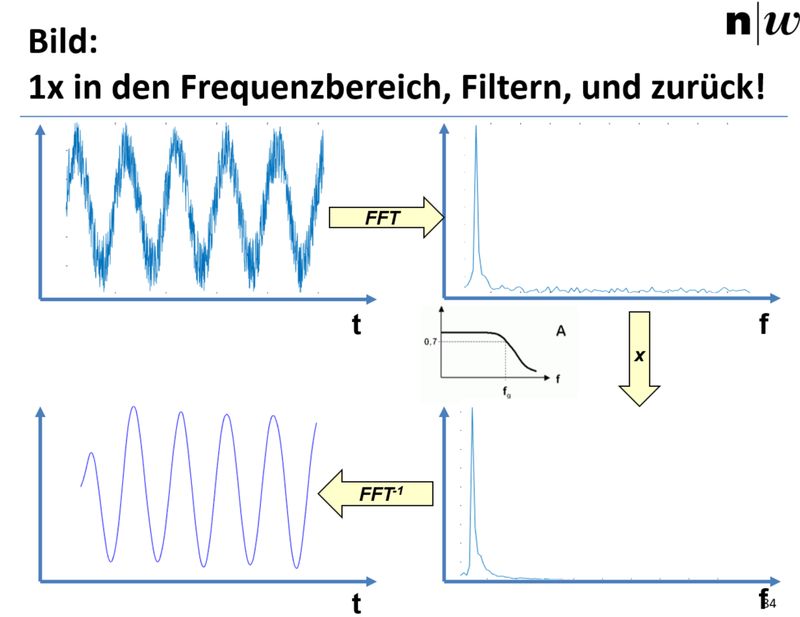
Für die Vorstellung finde ich das folgende Schema hilfreich: Es zeigt wie ein Signal von links oben im Zeitbereich mittels einer FFT (Fast Fourier Transform - dasselbe wie eine Fouriertransformation, nur geschickt gemacht und darum weniger rechenintensiv und daher "fast" genannt) in ein Signal im Frequenzbereich umgewandelt wird.Da das Signal im Wesentlichen ein verrauschter Sinus ist, bedeutet das dass es im Spektrum rechts oben einen deutlichen Peak hat bei der Frequenz des Sinus, und dazu hat es noch Rauschen das aus allen möglichen Frequenzen besteht. Das Rauschen ist hauptsächlich bei höheren Frequenzen als der Sinus selber (es "zappelt" wild innerhalb der Periode des Sinus). Dies sieht man im Spektrum als alle möglichen Frequenzen > der Signalfrequenz selber.
Im Frequenzbereich wird nun ein Tiefpassfilter angewendet, der dort einfach einer Multiplikation entspricht, und man landet rechts unten. Da der Tiefpassfilter Frequenzen grösser der Grenzfrequenz mit zunehmender Frequenz immer stärker dämpft, findet man noch ein bisschen etwas vom Rauschen übrig bei Frequenzen gerade neben dem Sinus, aber die hohen Frequenzanteile sind weg.
Transformiert man das Signal zurück, so findet man nun fast einen perfekten Sinus, weil die höherfrequenten Rauschanteile weg sind. Der Vergleich zum Originalsignal im Zeitbereich zeigt auch eine kleine Phasenverschiebung, wie erwartet.
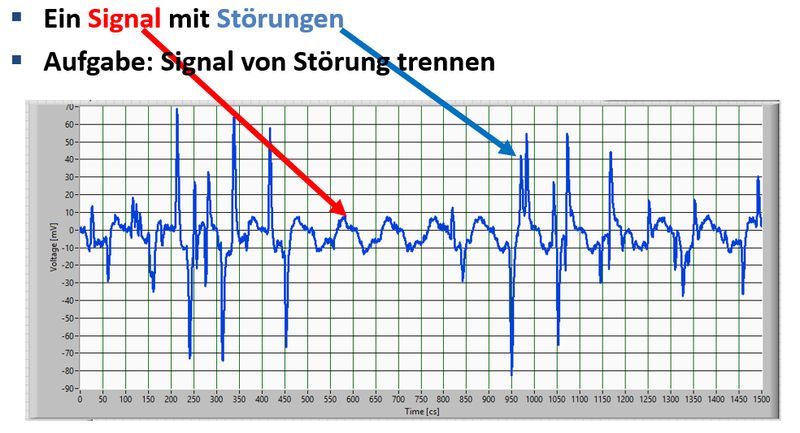
Ich habe Ihnen schon letztes Mal, und heute nochmals zu Beginn dieses Unterrichtsblocks dieses Bild mit einem Signal mit Störungen gezeigt. Nachdem Sie jetzt ganz viel gehört haben über die Frequenzanalyse - wie würden Sie das Signal bearbeiten um die Störungen loszuwerden? Seien Sie möglichst spezifisch, geben Sie z.B. auch die Grenzfrequenz des Filters an den Sie verwenden würden (x-Achse in cs beachten).
Lösung anzeigen
Lösen Sie zum Schluss bitte noch Übung 9 zum Thema Frequenzanalyse

