Impedanzmessungen + Sensoren die darauf beruhen
Einführung
In diesem Unterrichtsblock behandeln wir nach der bereits bekannten Messung von Widerständen zuerst die allgemeine Messung von Impedanzen, d.h. zusätzlich auch noch Kapazitäten und Induktivitäten; dann werden diverse Sensoren betrachtet die auf Kapazitäts- oder Induktivitätsänderungen basieren (insbesondere Abstandssensoren), und zuletzt werde ich Ihnen zeigen wie diese Sensoren elektronisch aufgebaut sind - dabei lernen oder repetieren Sie technisch wichtige Themen wie Schwingkreis, Resonanz und Wirbelstrom.
Resistive, induktive und kapazitive Sensoren
Wir haben bisher Temperatursensoren kennengelernt, die darauf beruhen, dass sich der Widerstand als Funktion der Temperatur verändert. Auf Englisch hiessen diese Sensoren "RTD" für "resistance temperature detector". Man kann ganz allgemein alle Sensoren, die auf Widerstandsänderungen beruhen, als "resistive Sensoren" bezeichnen. Ebenso gibt es Sensoren die auf Kapazitäts- oder Induktivitätsänderungen beruhen, und logischerweise bezeichnet man diese als "kapazitive Sensoren" oder "induktive Sensoren". Bevor wir ein paar Beispiele dazu anschauen, überlegen wir wie man Kapazitäten oder Induktivitäten überhaupt messen kann.Impedanzmessung
Sie haben bereits gelernt, dass man Widerstände messen kann, indem man sie an eine Konstantstromquelle mit definierten Strom \(I_0\) anschliesst, und die resultierende Spannung misst. Nun können wir uns fragen, wie man denn allgemeiner eine beliebige Impedanz \(Z\) misst, bzw. speziell wie man eine Kapazität \(C\) oder eine Induktivität \(L\) misst.Es gibt dazu verschiedene Prinzipien, aber am leichtesten zu verstehen ist sicher die Erweiterung der bisher bekannten Widerstandsmessung. Für eine Impedanz gilt ja \(U = ZI\) und damit kann man genau gleich wie bei der Widerstandsmessung vorgehen, mit einer kleinen Änderung.
Was muss gegenüber dem Widerstand verändert werden damit man eine Kapazität oder eine Induktivität messen kann?
Lösung anzeigen
Wir legen nun an einen Kondensator einen Wechselstrom an: \(I = I(t) = I_0 sin(\omega t)\), die Impedanz des Kondensators ist \(Z = {1 \over i \omega C}\), damit ergibt sich
\(C = {I \over \omega U}\)
Warum gilt diese Gleichung nicht exakt, sonder nur ungefähr?
Tipp anzeigen
Lösung anzeigen
Alternative Kapazitätsmessung durch Aufladen eines Kondensators
Normale Digitalmultimeter haben keine interne Wechselspannungsquelle, wohl aber eine präzise Gleichstromquelle zur Bestimmung von Widerständen. Die Gleichstromquelle kann zur Aufladung des Kondensators benützt werden, und damit auch zur Kapazitätsmessung. Wird ein Kondensator mit einem Strom \(I_0\) geladen, so gilt für die gemessene Kondensatorspannung \(U_C (t)\):\(U_C (t) = {I_0 \over C} t\)
Wird nun die Spannung als Funktion der Zeit gemessen während der Kondensator geladen wird, so kann aus dem Anstieg der Spannung die Kapazität berechnet werden. Es gibt dafür auch direkt integrierte Schaltungen (ICs) die solche Messungen durchführen – solche Bauteile können beispielsweise in der Auswerteelektronik von kapazitiven Sensoren eingesetzt werden. Das Bild zeigt einen solchen CU-Wandler.

Induktivitätsmessung
Die Impedanz einer idealen Spule ist \(Z = i \omega L\), und für Impedanzen gilt allgemein \(U = ZI\). Legt man eine Wechselspannung an einer Spule an, und misst dabei die Effektivwerte von Strom und Spannung, so gilt wieder näherungsweise\(L = {U \over \omega I}\)
Auch die Induktivitätsmessung kann also durch Messung von Wechselstrom und Wechselspannung geschehen – und wieder gilt die Gleichung nur ungefähr (warum?).
Selbstverständlich kann man auch (Wechselspannungs-)Messbrücken mit Kapazitäten oder Induktivitäten versehen und so kleine Änderungen von diesen Grössen bestimmen. Diese Technik wird in dieser Vorlesung nicht weiter besprochen, da wir schon die Messbrücke für Widerstandsänderungen kennengelernt haben; und ich möchte Ihnen bei der Kapazitäts- und Induktivitätsmessung weiter unten ein anderes Messprinzip (Schwingkreis/Resonanz) zeigen.
Potentiometer sind sehr beliebt als Weg- und Abstandssensoren, es gibt sie in Längen von mm bis Meter. Sie sind der "Default" für Abstandsmessungen. Das Bild unten zeigt einen potentiometrischen Wegsensor. Mit dem Gewinde auf der linken Seite wird er fix mit einem beweglichen Werkstück oder Maschinenteil verschraubt, dessen Bewegung dadurch zu der messbaren Widerstandsänderung führt. Auf der rechten Seite sieht man die 3 elektrischen Anschlüsse.
Zur Erhöhung der Messgenauigkeit wird das Potentiometer oft als Element einer Messbrücke eingesetzt.
\(C = {A \varepsilon \varepsilon_0 \over d}\)
Für Kondensatoren mit anderer Geometrie ist die Lage ähnlich, darum wird hier nur auf den Plattenkondensator eingegangen. Die Kapazität kann also durch alle drei Grössen \(A, \varepsilon, d\) beeinflusst werden. Damit ergeben sich vielfältige Konstruktions- und auch Anwendungsmöglichkeiten für kapazitive Sensoren:
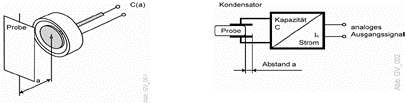
Das nächste Bild zeigt einen typischen kapazitiven Abstandssensor mit Aussengewinde für leichten Einbau. Der Kondensator (genau wie im Bild oben aufgebaut) befindet sich links in der grünen Kappe, geschützt vor äusseren Einflüssen – Gegenstände die von links auf diese Kappe zubewegt werden, werden vom Sensor erkannt.
Beispiele für Sensoren die auf RLC-Messungen beruhen
Resisitive Sensoren
Als resistive Sensoren bezeichet man Sensoren die auf Widerstandsänderungen beruhen. Beispiele dafür sind:
Das Bild unten zeigt den Aufbau eines linearen Potentiometers: Je weiter oben im Bild der Schleifer ist, desto grösser ist die gemessene Spannung. Das Potentiometer ist also einfach ein Spannungsteiler. Aus der Spannungsmessung lässt sich leicht der Abstand rekonstruieren.

Kapazitive Sensoren
Kapazitive Sensoren beruhen auf der Messung einer Kapazität (bzw. ihrer Änderung). Die Kapazität eines Plattenkondensators mit Fläche A und Abstand d zwischen den Platten ist gegeben durch
Das Bild unten zeigt links die geometrische Anordnung der beiden Elektroden eines kapazitiven Abstandssensors; und rechts das Prinzipschema dazu, wo der Kondensator als Plattenkondensator dargestellt ist. Das elektrische Feld im realen Sensor ist zwischen den beiden Elektroden, d.h. zwischen der grauen runden Elektrode innen, und der äusseren weissen "offenen Büchse". Natürlich ist das Feld am stärksten direkt im Inneren dieser weissen Büchse, aber ein paar Feldlinien ragen auch nach vorne heraus, so dass ein Objekt das sich nähert, das elektrische Feld stört und damit die Kapazität dieses Kondensators erhöht.

Dielektrizitätskonstanten
Kapazitive Abstandssensoren haben den grossen Vorteil dass sie (im Gegensatz zum Potentiometer oben) ohne bewegliche Teile auskommen. Sie werden nur durch die relative Dielektrizitätskonstante (oder "relative Permittivität") des Messobjekts beeinflusst. Um kapazitive Abstandssensoren besser zu verstehen muss man wissen wie gross \(\varepsilon\) etwa sein kann, denn die Kapazität eines Kondensators ist ja proportional zu \(\varepsilon\) - kapazitive Sensoren reagieren also nicht auf alle Materialien gleich! Die folgende Tabelle aus Wikipedia gibt uns einen Anhaltspunkt:
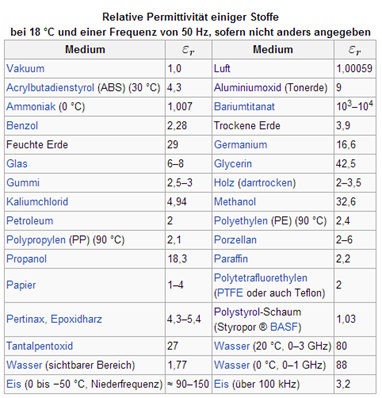
Welche Substanzen kann man mit kapazitiven Sensoren besonders gut erfassen? Und warum ist die Dielektrizitätskonstante von Styropor so tief?
Styropor besteht hauptsächlich aus Luft, darum hat es so eine tiefe Dielektrizitätskonstante.
Lösung anzeigen
- Gase haben eine relative Dielektrizitätskonstante von ganz wenig mehr als 1
- Viele Feststoffe haben einstellige \(\varepsilon\)
- Wasser hat eine auffällig hohe relative Dielektrizitätskonstante, was sich zB auch im Unterschied feuchte Erde zu trockene Erde bemerkbar macht.
- Metalle kommen in der Tabelle nicht vor, weil die relative Dielektrizitätskonstante eben für "Dielektrika" angebeben wird, d.h. für isolierende Stoffe. Stellt man sich die relative Dielektrizitätskonstante so vor dass sie von der Polarisierbarkeit stammt, so ist klar dass \(\varepsilon\) für ein Metall theoretisch unendlich gross ist.
Daraus können wir die folgenden allgemeinen Eigenschaften von kapazitiven Abstandssensoren ableiten: Kapazitive Abstandssensoren reagieren auf praktisch alle Feststoffe, nicht aber auf Gase. Sie reagieren besonders stark auf Metalle. Sie können durch Feuchtigkeit (Spritz- und Kondenswasser) gestört werden; umgekeht kann man natürlich leicht Feuchtesensoren bauen die auf einer kapazitiven Messung beruhen.
Da \(\varepsilon\) eine Materialeigenschaft ist, reagieren kapazitive Abstandssensoren für unterschiedliche Materialien stärker oder schwächer, je nach \(\varepsilon\) des Materials das sich nähert. Da elektrische Felder in Dielektrika eindringen, wird der Sensor auf dicke Objekte stärker reagieren als auf dünne.
Im Video zeige ich Ihnen diese Dinge anhand eines Demo-Abstandssensors im Mess- und Sensortechniklabor.
Auswerteschaltung
Wir haben bereits gesehen dass man die Kapazität eines Kondensators prinzipiell mit Wechselstrom mit Hilfe von \(U = ZI\) bestimmen kann. Für die Auswertung von kapazitiven Sensoren werden aber direkt C-U-Umsetzer verwendet, oder Schwingkreise. Im Video haben Sie gehört wie der Demo-Sensor ein Geräusch macht, dessen Frequenz umso höher ist je grösser der Messeffekt ist. Diese Auswerteschaltung misst die Frequenz eines Schwingkreises, und gibt ihre Differenz zu der "ungestörten" Frequenz auf dem Lautsprecher aus. Der Schwingkreis wird beim induktiven Sensor noch genauer diskutiert.Induktive Sensoren
Induktive Sensoren arbeiten mit Spulen anstatt mit Kondensatoren. Ähnlich wie bei resistiven und kapazitiven Sensoren die kleine Änderungen von \(R\) und \(C\) messen, kann man sich vorstellen dass induktive Sensoren kleine Änderungen von \(L\) messen. Dies ist aber nur die halbe Wahrheit: Die Induktivität von Spulen lässt sich zwar tatsächlich dadurch beeinflussen dass man einen Eisenkern in eine Spule einbringt, und es gibt Sensoren die so arbeiten (sogenannte Tauchanker-Aufnehmer); aber die meisten induktiven Sensoren funktionieren anders. Im Tauchanker-Aufnehmer erhöht der Eisenkern die Induktivität der Spule, was gemessen + ausgewertet werden kann. Dieser Sensor hat aber wie oben schon bei den resistiven Sensoren gesehen den Nachteil dass er einen beweglichen Teil enthält.Im Bild unten ist ein sogenannter Tauchanker-Sensor gezeigt. Ein Eisenkern wird um die Strecke \(l-s\) in die Spule der Länge \(l\) mit \(N\) Windungen eingebracht, und verändert dadurch die Induktivität der Spule.
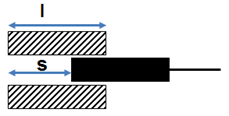
Bei den kapazitiven Sensoren war die Dielektrizitätskonstante \(\varepsilon\) die ausschlaggebende Materialeigenschaft, bei dem Eisenkern ist es seine magnetische Permeabilität \(\mu\). Auch hier lohnt sich ein Blick in eine Tabelle aus Wikipedia um festzustellen was für Materialien ausser Eisen man so nachweisen könnte:
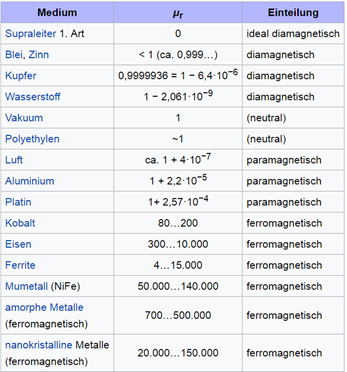
Man sieht dieser Tabelle an, dass \(\mu\) für fast alle Materialien ziemlich genau 1 ist. Nur eine ganz besondere Klasse von Materialien – die Ferromagnete – haben "grosse" \(\mu\). Dazu gehören nur 3 reine Elemente, nämlich Eisen, Kobalt und Nickel. Alle anderen reinen Metalle haben \(\mu \approx 1\).
Will man den Tauchanker-Sensor beschreiben, so muss man wissen wie ein Material mit \(\mu >> 1\) (wie der Eisenkern) die Induktivität der Spule verändert. Dazu gibt es folgende Näherungsformel:
\(L \approx {\mu_0 N^2 A \over s}\)
wobei \(s\) die Länge des Luftraums innerhalb der Spule ist. \(\mu\) selber kommt in der Formel nicht vor, da es als quasi unendlich angenommen wurde. Materialien mit \(\mu \approx 1\) können die Induktivität der Spule hingegen nicht verändern, und könnten so nicht detektiert werden. Trotzdem gibt es berührungslose induktive Abstandssensoren, die von aussen genau gleich aussehen wie die oben beschriebenen kapazitiven Abstandssensoren. Sie werden besonders in Maschinenanlagen zu Millionen verbaut und erkennen zuverlässig alle Metalle, nicht nur ferromagnetische Metalle! Sie arbeiten nicht mit einer direkten Induktivitätsmessung der Spule!
Induktive Abstandssensoren
Die induktiven Abstandssensoren sind so aufgebaut dass das Magnetfeld einer Spule aus dem Sensor austritt – ähnlich wie beim kapazitiven Sensor das elektrische Feld austritt. Dies ist im Bild unten gezeigt, links ist ein induktiver Abstandssensor ohne, rechts mit einer Abschirmung dargestellt. Quelle.

Die Abschirmung des Felds wie rechts im Bild gezeigt, dient dazu dass der Sensor in ein metallisches Objekt bündig eingebaut werden kann, ohne dass er dauernd angibt; der Aufbau links würde vom metallischen Objekt in das er eingebaut würde bereits dauernd ein Signal ausgeben. Diese induktiven Abstandssensoren gibt es in einer Vielzahl von Ausführungen damit sie auch in jeder möglichen Anwendung gut eingebaut werden können. Ein Beispiel für die vielfältigen Bauformen solcher Sensoren ist im Bild unten gezeigt. Quelle.

Auswerteschaltung induktiver Sensoren
Nach den bisherigen Ausführungen ist klar, dass die induktiven Sensoren für nicht-ferromagnetische Materialien im Einflussbereich des Sensors gar keine Veränderung der Induktivität messen können. Trotzdem erfassen sie zuverlässig alle Metalle – wie kann das gehen? Hier nutzt man mehrere Phänomene, die Sie vielleicht aus anderen Modulen bereits kennen – darum ist es schön diese Anwendung der ehemals eventuell trockenen Theorie anzuschauen.In der Physik haben Sie vermutlich das Pendel kennengelernt – entweder als Fadenpendel oder als Federpendel. Charakteristisch für das Federpendel ist dass es eine rücktreibende Kraft hat, die proportional zu der Auslenkung ist: \(F = -kx\). Damit ergibt sich mit Hilfe von \(F = ma\) die Differentialgleichung:
\(F = ma = m \ddot x = -kx\)
Oder
\(\ddot x = -{k \over m}x\)
Für das Fadenpendel gilt näherungsweise dasselbe für den Winkel \(\alpha\) statt für den Weg \(x\).
Dies erinnert Sie ans Kapitel 2 und die Differentialgleichung für das Verhalten des Temperatursensors (oder von Aufladungsvorgängen von Kondensatoren, oder von radioaktiven Zerfällen). Diesmal steht links allerdings die zweite Ableitung nach der Zeit da.
Klassifizieren Sie diese Differentialgleichung (geben Sie ihr einen Namen)!
Tipp anzeigen
Lösung anzeigen
Was ist einfacher zu lösen: eine homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, oder eine inhomogene Differentialgleichung erster Ordnung mit konstanten Koeffizienten?
Lösung anzeigen
Tipp anzeigen
\(x(t) = e^\lambda t\)
Setzen Sie diese Funktion \(x(t)\) in die Differentialgleichung ein und schauen Sie was dann passiert (die zweite Ableitung können Sie nun berechnen).
Lösung anzeigen
\(\lambda = \sqrt {-{k \over m}}\)
\(x(t) = x_0 sin(\omega_0 t) ; \quad \omega_0 = \sqrt {k \over m}\)
\(\omega_0\) ist die Kreisfrequenz der Schwingung.
Der elektrische Schwingkreis
In der Elektrotechnik gibt es eine einfache und schöne Entsprechung zum mechanischen Pendel, den sogenannten LC-Schwingkreis (Bild aus Wikipedia):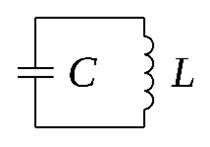
Tipp anzeigen
Lösung anzeigen
Setzt man die Spannungen für Kondensator und Spule ein, so erhält man:
\(L \dot I = - {Q \over C}\)
Aus dem zweiten Teil vom Tipp: Der Strom ist die Ableitung der Ladung nach der Zeit: \(L\dot Q = I\) ergibt sich nach einsetzen:
\(L\ddot Q = -{Q \over C}\)
\(\ddot Q = -{1 \over LC}Q\)
Damit haben wir eine Differentialgleichung gefunden die exakt gleich aussieht wie die Differentialgleichung für das mechanische Pendel, nur die Buchstaben heissen anders: beim Pendel hatten wir eine Auslenkung \(x\), zu der beim Schwingkreis die Ladung \(Q\) im Kondensator analog ist; und beim Pendel hatten wir Federkonstante und Masse, die die Zeitkonstante der Schwingung bestimmt haben - hier sind es die (reziproke) Kapazität und die Induktivität die den mechanischen Grössen Federkonstante und Masse entsprechen.
Der elektrische Schwingkreis verhält sich also exakt analog zum mechanischen Schwingkreis, er produziert eine Schwingung mit der Frequenz
\(\omega_0 = \sqrt{1 \over LC}\)
Resonanz
Jedes schwingungsfähige System schwingt von sich aus mit einer natürlichen Kreisfrequenz, die wir oben berechnet haben. Setzt man ein Kind auf eine Schaukel, und stösst es einmal mit einem Kraftimpuls an, so führt diese Schaukel eine "freie Schwingung" mit ihrer natürlichen Frequenz durch.Durch Reibung wird die Amplitude der Schaukelbewegung mit der Zeit kleiner, und das Kind unzufrieden. Darum muss man dem System Schaukel+Kind laufend weiter Energie zuführen, man spricht dann von einer erzwungenen Schwingung.
Wird ein schwingungsfähiges System mit einer äusseren Kraft mit Kreisfrequenz \(\omega\) angeregt, so schwingt es ebenfalls mit dieser Kreisfrequenz mit – auch wenn seine natürliche Kreisfrequenz \(\omega_0\) nicht gleich \(\omega\) ist. Nähert man sich der natürlichen Kreisfrequenz \(\omega_0\) des Systems (auch Eigenfrequenz genannt), so wird die Amplitude der Schwingung immer grösser.
Auf den Spielplatz übertragen: gibt man dem Kind auf der Schaukel in der richtigen Frequenz an, so kann es sehr stark schaukeln.
Bitte schauen Sie auf dem Videoportal der Uni Freiburg das Video zu der erzwungenen Schwingung - beobachten Sie, was mit der Amplitude und der Phasenlage Anregung-Schwingung passiert, wenn die Frequenz der Anregung langsam erhöht wird!
Übertreibt man, so kann es zu einer sogenannten Resonanzkatastrophe kommen: die Amplitude wird immer grösser, bis sich das System aufgrund der grossen Amplitude selbst zerstört. Ein bekanntes Beispiel kommt aus dem Militär, wo Soldaten nicht im Gleichschritt über Brücken marschieren dürfen, weil sie die Brücke so zum Schwingen anregen könnten, dass sie zusammenbricht (tatsächlich 1831 in England passiert). Ein anderes sehr berühmtes Beispiel mit einer einstürzenden Brücke ist im Video unten gezeigt, die Tacoma Narrows Bridge, die schon kurz nach ihrem Bau eingestürzt ist. Es ist zwar kein besonders gutes Beispiel für die Resonanzkatastrophe, da es mehr mit aerodynamischem Flattern zu tun habe, aber das Video ist trotzdem beeindruckend.
Ein weiteres bekanntes Beispiel ist die Bodenresonanz von Helikoptern, im Video unten können Sie einige Beispiele davon sehen.
Gedämpfte Resonanz
In der Natur ist jede Schwingung in irgendeiner Form gedämpft. Das mechanische Pendel ist über Reibung (Luftwiderstand) gedämpft, der Schwingkreis ist über den elektrischen Widerstand der elektrischen Leiter gedämpft. Um ein echtes System darzustellen, müsste man auch noch einen elektrischen Widerstand in den Schaltkreis des Schwingkreises einzeichnen, so dass \(R, L\) und \(C\) in Serie geschaltet wären. Freie gedämpfte Schwingungen haben eine Amplitude die mit der Zeit kleiner wird (exponentieller Abfall gegen 0, Pendel das einmal ausgelenkt und losgelassen wird), für uns interessant ist jedoch dass sich aufgrund der Dämpfung die Resonanzkurve des Systems bei erzwungener Schwingung ändert. Das Bild der Uni Göttingen zeigt dies:
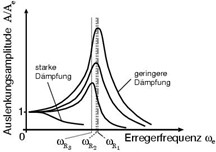
Die Abbildung zeigt wie bei geringer Dämpfung die Amplitude hoch ist; die Resonanzkurve hat ein ausgeprägtes und schmales Maximum. Mit zunehmender Dämpfung wird die Amplitude der erzwungenen Schwingung bei gleichbleibender Anregung kleiner, ebenso verschiebt sich die Frequenz, bei der die maximale Amplitude erzeugt wird, zu tieferen Frequenzen; und die Resonanzkurve verbreitert sich. Genau diesen Effekt nutzt man im induktiven Sensor aus, um alle Metalle und nicht nur die speziellen ferromagnetischen Metalle zu detektieren.
Aufbau induktiver Sensor
Im Bild unten ist der Aufbau eines modernen induktiven Sensors der Firma Baumer gezeigt. Der Sensor hat intern einen Oszillator (LC-Schwingkreis) dessen Schwingung ausserhalb vom Sensor von einem metallischen Objekt gedämpft werden kann.
Der Sensor detektiert sowohl die Änderungen der Amplitude wie auch der Frequenz, um daraus sein Signal zu generieren.
Wirbelströme
Die Dämpfung des Schwingkreises erfolgt folgendermassen: das magnetische Wechselfeld induziert im metallischen Objekt, das sich dem Sensor nähert, Wirbelströme. Diese Wirbelströme werden durch den elektrischen Widerstand des metallischen Objekts wiederum gedämpft, wodurch das metallische Objekt dem Sensor laufend Energie entzieht – und damit eben den Schwingkreis dämpft. Man kann also an der reduzierten Amplitude oder einer tieferen Frequenz im Schwingkreis erkennen, dass ein elektrisch leitfähiges Objekt im Magnetfeld des Sensors ist.Die gesamte Diskussion über die Auswertung der induktiven Sensoren lässt sich 1:1 auch auf kapazitive Abstandssensoren übertragen! Wenn anstelle der Induktivität der Spule im LC-Kreis die Kapazität des Kondensators verändert wird, passiert exakt dasselbe, die gesamte Auswertung über die Änderung der Amplitude oder Frequenz des Schwingkreises bleibt gleich.
Im Video zeige ich Ihnen einen Laboraufbau eines Schwingkreises, und wie er auf verschiedene Metalle reagiert. Der Schwingkreis ist wie folgt aufgebaut:
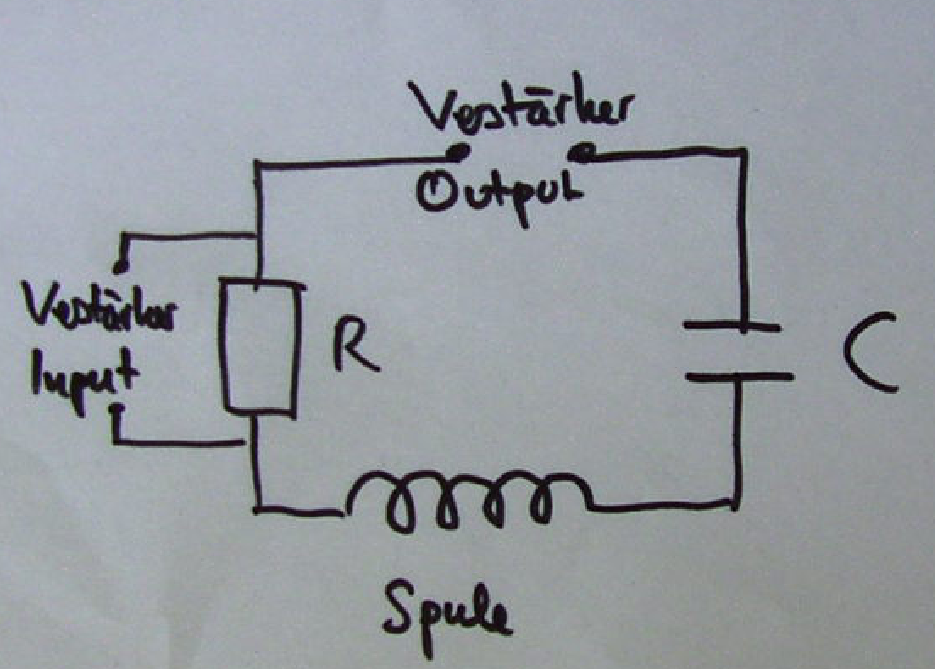
Wie Sie im Video schön gesehen haben, reagiert unser Schwingkreis viel stärker, wenn das nichtmagnetische Metallobjekt auf die Spule gelegt wird, als wenn es senkrecht in die Spule eingebracht wird. Der Grund dafür ist, dass sich die Wirbelströme viel weniger gut ausbilden können, da sie sich gerne ähnlich kreisförmig bewegen würden, wie die Spule hingelegt ist. Im flach aufgelegten Metall können Sie das, im senkrecht gestellten Metall ist ihre Bewegung behindert. Dadurch sind die induzierten Wirbelströme kleiner, und entsprechend ist die Dämpfung des Schwingkreises kleiner. Dies ist technisch von sehr grosser Bedeutung in Transformatoren, wo die Eisenkerne "geblecht" sind, damit die Verluste durch die Wirbelströme möglichst gering sind. Ebenso ist es in Elektromotoren / Generatoren wichtig - für Details s. Wikipedia zu Elektroblech.
Im Video zeige ich Ihnen als Letztes noch einen Metalldetektor, und dass er auf alle Metalle reagiert.
Zusammenfassung
Induktive Sensoren reagieren also – erstaunlicherweise – nicht primär auf die magnetische Permeabilität \(\mu\), wie man aufgrund der Gleichung für die Induktivität einer Spule meinen könnte, sondern hauptsächlich auf die elektrische Leitfähigkeit des Messobjekts. Dadurch lassen sich alle metallischen Objekte problemlos erkennen, aber auch sonstige leitfähige Materialien wie Graphit. Sie reagieren jedoch auf alle nichtleitenden Stoffe gar nicht, und sind darum deutlich selektiver als die kapazitiven Sensoren. Anders als kapazitive Sensoren sind sie daher unempfindlich gegen Verschutzung, Spritzwasser, und Luftfeuchtigkeit, und darum besonders robust in einem industriellen Umfeld. Da die Sensoren durch den elektrischen Widerstand eines sich nähernden Objekts gedämpft werden, reagieren sie meistens auf unterschiedliche Metalle unterschiedlich stark. Je grösser der Widerstand im Metall, desto grösser der Energieverlust und desto stärker die Dämpfung. Wie im Video mit dem Demo-Versuch zu sehen war, reagieren die Sensoren aber durchaus auch auf \(\mu\): Eisen verhält sich anders als nichtmagnetische Metalle.Ich hoffe, Sie haben bemerkt, wie wunderschön man an den heute behandelten Sensoren sieht, dass die Sensortechnik ein Fach ist, das auf ganz vielen Grundlagen aufbaut: Wir haben aus der Mathematik Differentialgleichungen benützt, aus der Physik elektrische und magnetische Felder, induzierte Ströme, Ohmsche Verluste, Schwingungen und Resonanz; und aus der Elektrotechnik die Maschenregel und RC- sowie LC-Schaltungen. Alle diese Grundlagen sind wichtig, was man oft nicht so gut sieht wenn man das entsprechende Fach besucht ("wofür ist das gut??") - aber bei uns in der Sensortechnik kann man alles miteinander zu einer richtigen Anwendung verbinden!
Trotzdem ist das Fach ja Sensortechnik, versuchen Sie also nochmals darüber nachzudenken was dies alles mit Abstandssensoren zu tun hat:
Sie haben in diesem Kapitel 3 verschiedene Sensoren kennengelernt mit denen Abstände oder Wege gemessen werden können – Potentiometer, kapazitive Abstandssensoren und induktive Abstandssensoren. Versuchen Sie sich aufgrund der Theorie oben zu überlegen, welche Vor- und Nachteile diese Sensortypen haben!
Tipp anzeigen
Lösen Sie bitte im Anschluss an das Theoriestudium die Übung 7!

